" 조화란 수 많은 것들이 혼합된 것 속의 통일이며, 다양한 뜻을 지닌 것들 사이에서 일어나는 의미의 결합이다. " - 피타고라스
.. 라반은 움직임을 연구하기 위해 고대 그리스 철학자들이 추구하는 조화와 비례의 미를 받아들였고, 이를 통해 움직임에서 볼 수 있는 조화로운 형식을 찾고자 하였다. 그는 공간 안에서 이루어지는 조화로운 움직임이 다양한 기하학적 형태의 비례와 균형의 원리를 통해 연구될 수 있다고 가정하고 공간 안에서 수없이 창조되는 움직임이 남기는 흔적의 형태들(trace-forms)을 연구했다. 라반은 이것을 Choreutics 또는 Space Harmony로 명명하고, 공간 속에서 만들어지는 움직임의 다양한 형태들에 대해 좀 더 실질적으로 분석하고 연구할 수 있는 기초 개념을 확립했다..
.. 라반의 공간은 무게 중심의 이동 없이 인간의 사지가 가장 가까이 혹은 가장 멀리 도달할 수 있는 공간인 개인 공간 혹은 Kinesphere와 무게 중심이 이동하면서 만들어지는 일반 공간을 나누었다. 우리의 몸은 제자리에 머물러 있거나 움직일 때에도 항상 개인 공간이 둘러싸고 있다. 움직이는 사람의 에포트나 긴장 등이 개인 공간을 채울 때, 이를 역동 공간(Dynamosphere)이 창조된다고 말한다.. 개인 공간은 무게 이동 없이 가장 먼 거리까지 몸을 펼칠 수 있는 공간이고, 일반 공간은 몸의 무게 이동과 함께 개인 공간이 움직일 수 있는 무한대의 공간이라고 설명할 수 있다..
.. 라반의 공간 조화는 인간의 몸 움직임이 일어날 수 있는 잠재적 공간인 개인 공간에서의 움직임에 대한 연구로 이루어진다.. 움직임을 통해 몸이 점유할 수 있는 무한한 공간이 존재하지만, 라반은 이러한 공간 연구를 위해 기록하거나 분석하기 쉽도록 공간을 27개의 방향과 세 가지 종류의 높낮이로 구분했다.. 무게 중심을 옮길 때에는 기호의 색깔에 따라 높은 / 중간 / 낮은 높이로 걷게 되지만, 무게 이동과 무관한 사지의 제스처를 할 경우에는 몸의 각 부위 별로 정해진 기준점에서 높낮이를 정한다..


개인 공간에서의 움직임 / 스케일
.. 라반은 기하학에 근거해 공간 상에서 나타나는 조화로운 움직임의 구조와 특질을 설명했다. 정다면체를 통해 설명하면서, 이것을 움직임의 결정체라고 명명하였다. 인간이 움직임에서 사용하는 공간들을 연결하면 일정한 형상이 만들어 지는데 이를 움직임의 결정체라고 하며.. 이러한 결정체들 안에서 움ㅈ기임의 요소를 결합하고 조직화하는 과정에서 다양한 특성을 가진 공간 상의 스케일을 만들 수 있다..
.. 1차원의 움직임은 수직축, 수평축, 시상축 상에서 일어나는 움직임을 말한다.. 세 축의 양 끝 방향을 오가며 6개의 방향을 이어가는 공간적 움직임이 가능하고.. 1차원의 선의 움직임은 Dimensional(디멘셔널) 스케일 혹은 Defense(디펜스) 스케일을 만든다. 이는 정팔면체 상에서 나타나는 움직임이다.

.. 2차원의 움직임은 수직면, 수평면, 시상면의 세 개의 평면에서 이루어진다. 각 평면은 2개의 선이 만나 꼭지점을 이루며 2개의 공간적 당김을 갖게 되어 움직임도 2차원적 특질을 갖게 된다.. 2차원의 평면들은 정사각형이 아닌 직사각형을 이루는데, 각 면에서 두 개의 긴 선과 두 개의 짧은 선의 길이는 황금 비율의 조화로 이루어져 있다. 그래서 수직면, 수평면, 시상면의 각 꼭지점으로 이루어진 정이십면체 상에서 조화롭고 안정적인 움직임을 만들 수 있다.. 2차원의 평면에서 만들어지는 각각의 대각선을 Diameteral이라고 한다.


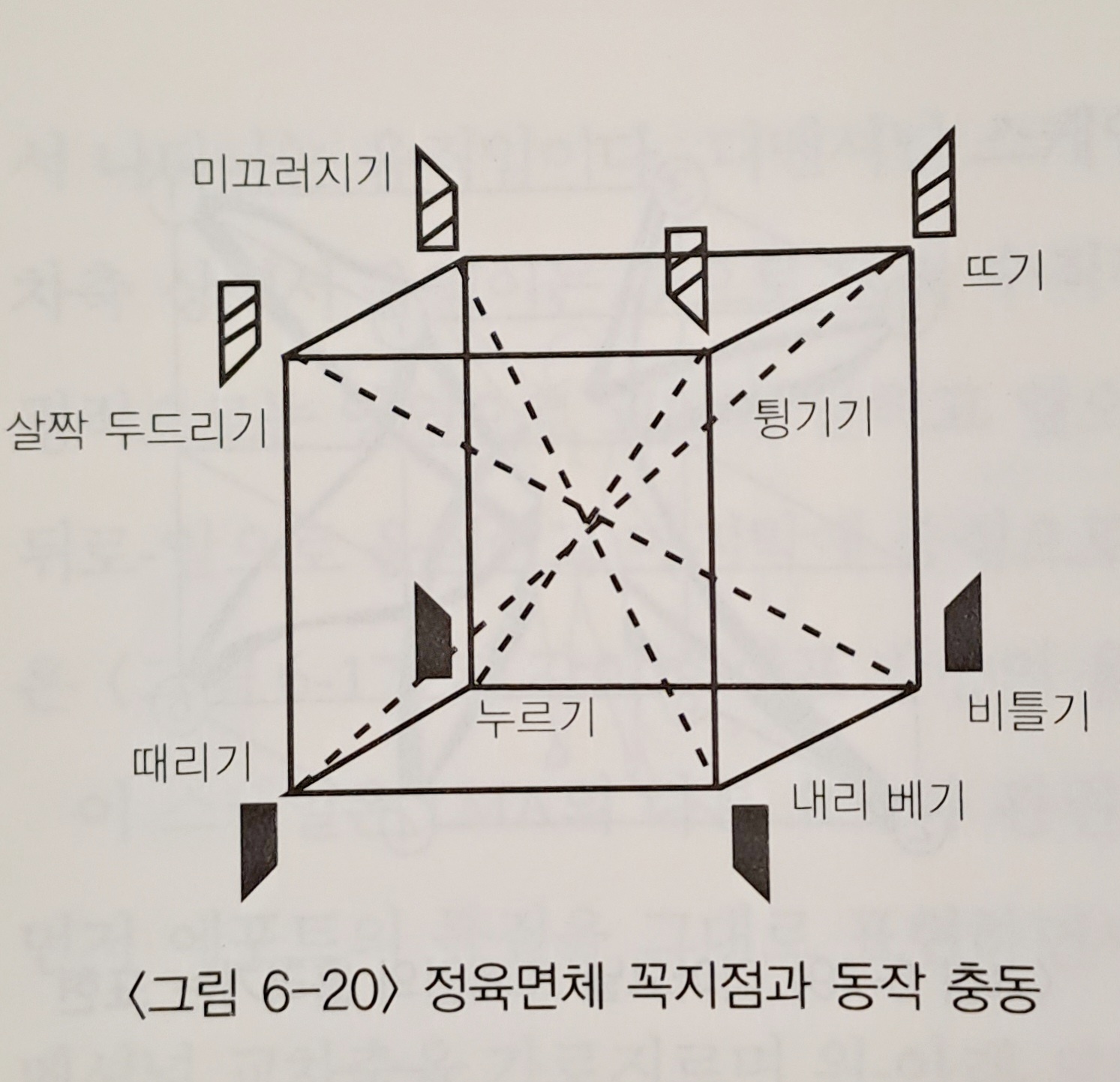
.. 정육면체의 3차원적 공간 안에서는 수직선, 수평선, 그리고 시상선이 동시에 만나는 꼭지점이 8개를 향해 가는 움직임을 만들 수 있다. 이 정육면체를 구성하는 하나의 꼭지점은 수직, 수평, 시상선의 당김이 모여서 이루어지므로 세 개의 공간적 당김을 갖게 된다.. 여기서 발생되는 공간적 당김은 2차원의 평면에서 두 선이 서로 다른 당김 비율을 갖는 것과는 달리 수직선, 수평선, 시상선의 당기는 힘이 같다.. 3차원의 정육면체에서는 Diagonal(디아고널) 스케일이 만들어 진다.

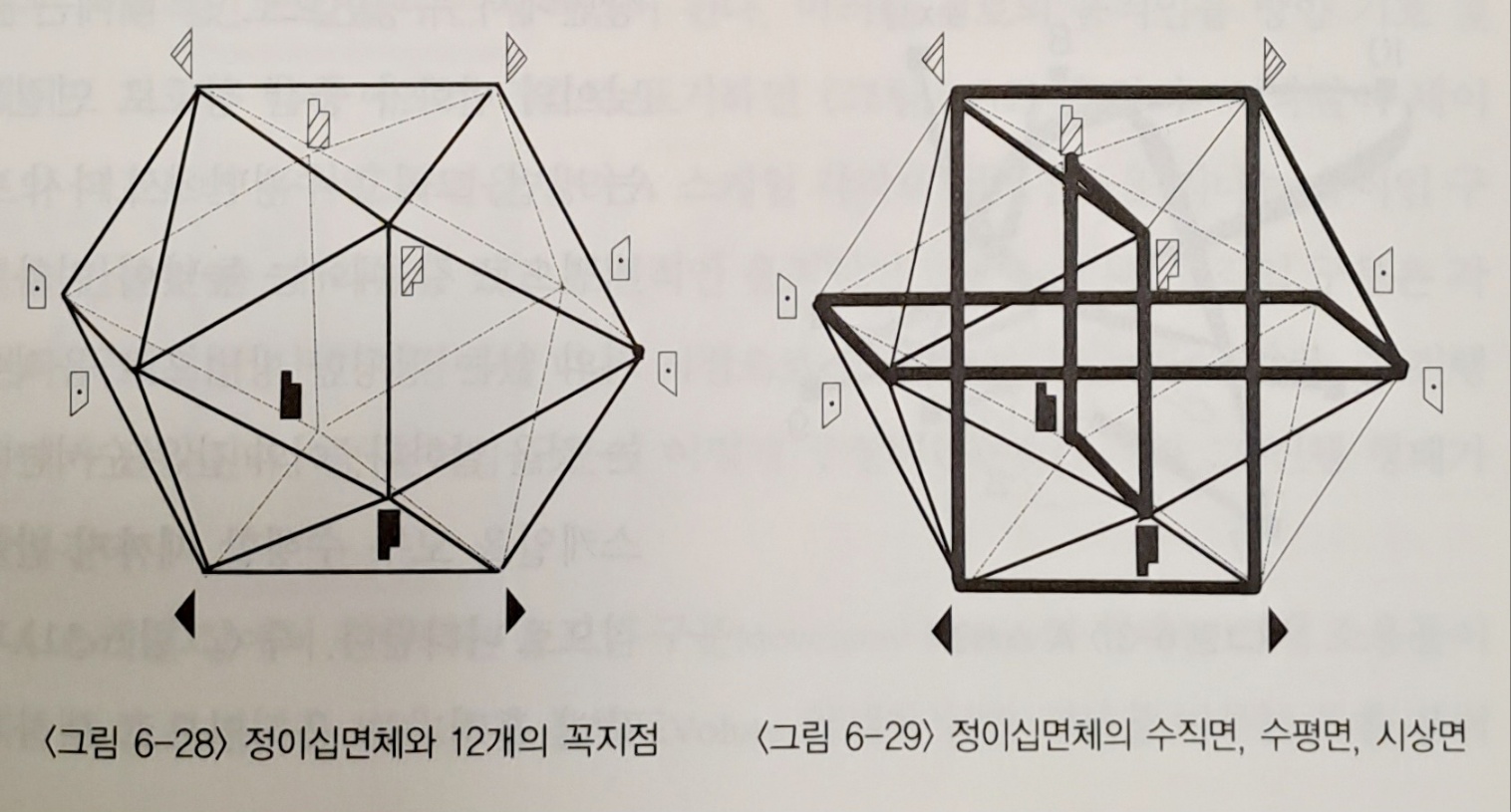
.. 정이십면체는 수직면, 수평면, 시상면의 2차원 평면이 교차하여 존재하는 12개의 꼭지점들을 연결하여 구성되어 있다. 정이십면체의 스케일은 Axis, Girdle, Primary, A, B, C, D 스케일 등으로 구성된다..
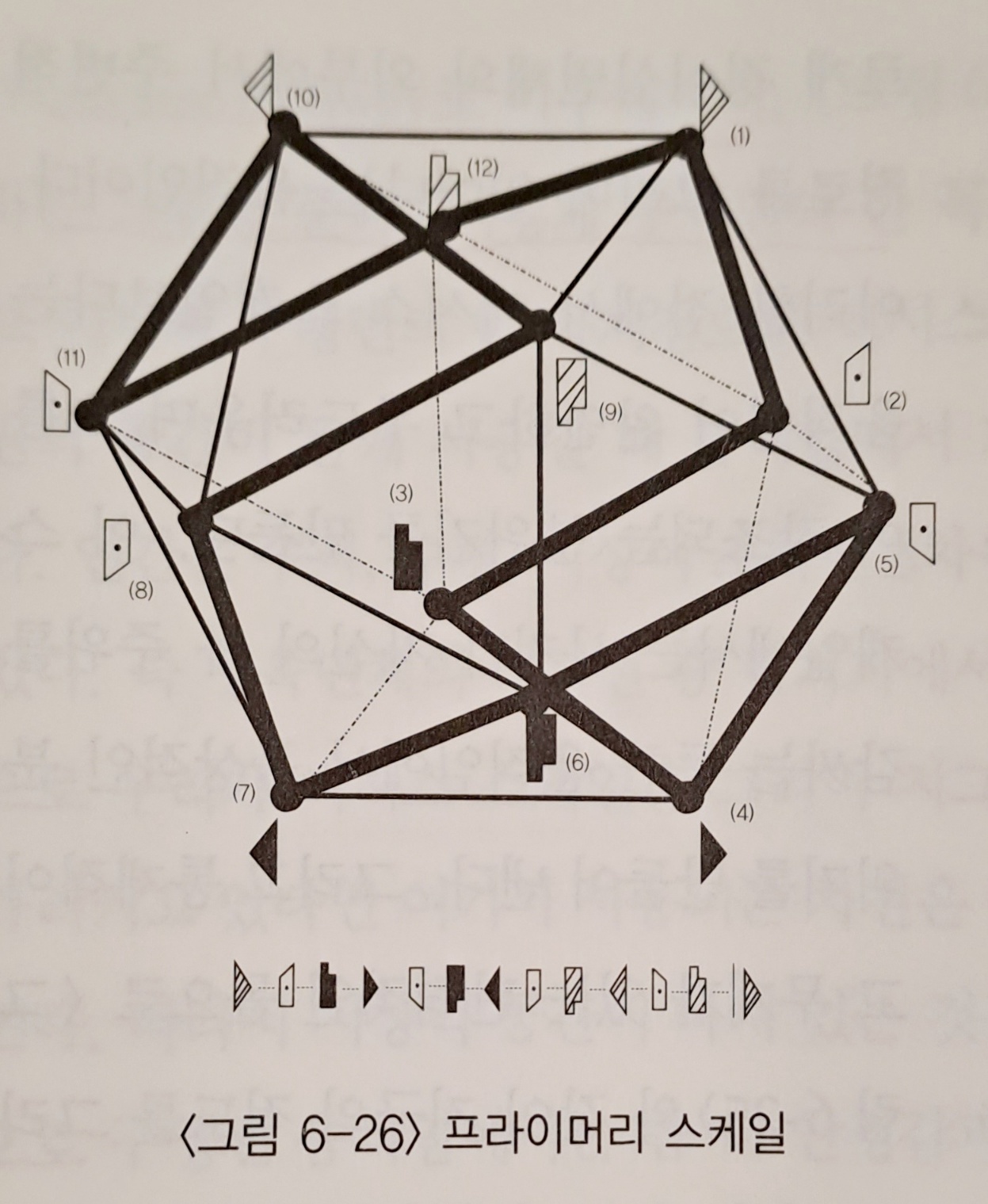
- Primary scale : 정육면체의 대각선 네 개 중 한 축을 기준으로 이를 둘러싸고 있는 꼭지점들을 연결한 조합으로 이루어져 있다. 각 축은 하나의 독립된 스케일을 가지므로, 모두 네 개의 스케일을 만들어 낸다. Axis와 Girdle 스케일을 이루는 꼭지점 모두를 지나게 된다. 횡단적 경로로 이루어진 Axis 스케일과 주변적 경로로 이루어진 Girdle 스케일의 각 꼭지점들을 번갈아가며 지나는 움직임의 조합을 만든다.
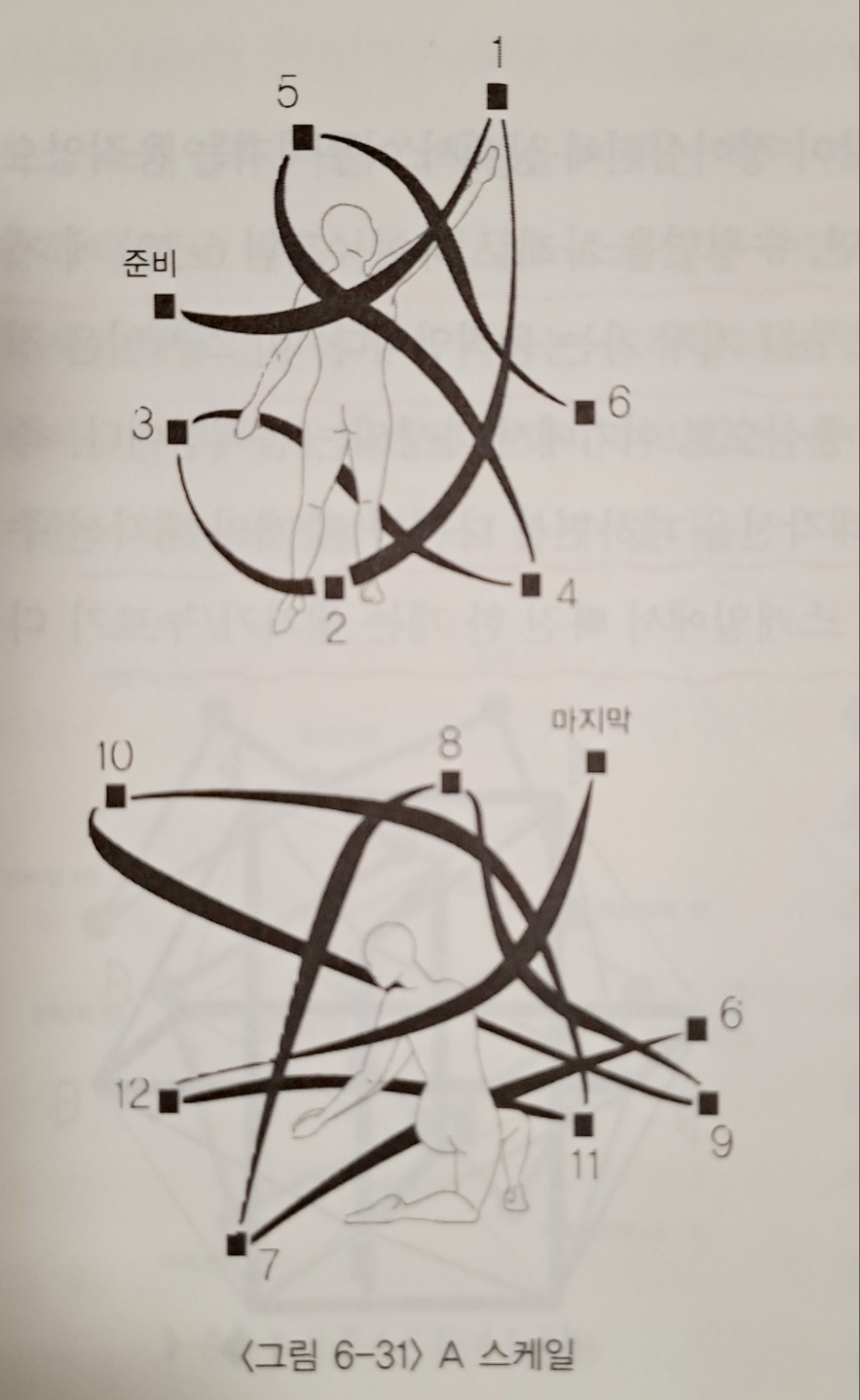
- A scale : 정육면체의 대각선 중 한 가지 (튕기기/ 누르기 디아고널)를 피하면서 나머지 세 개의 대각선 주위를 돌면서 스케일이 만들어 진다. 수직면-시상면-수평면을 연속적으로 반복하면서 진행되며, 2차원적인 평면의 꼭지점들을 지나가는 서정적이고 여성적인 느낌을 준다..
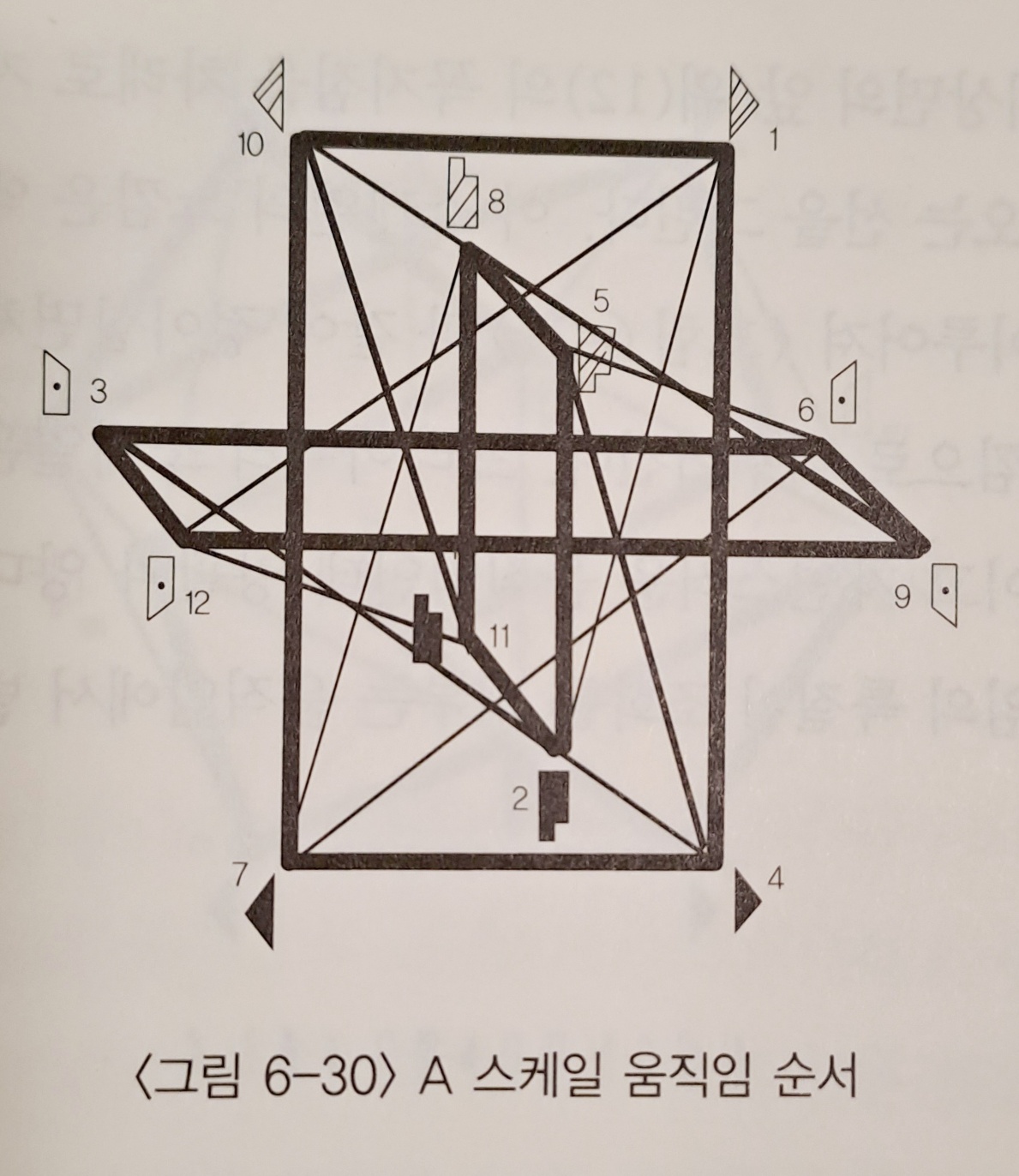
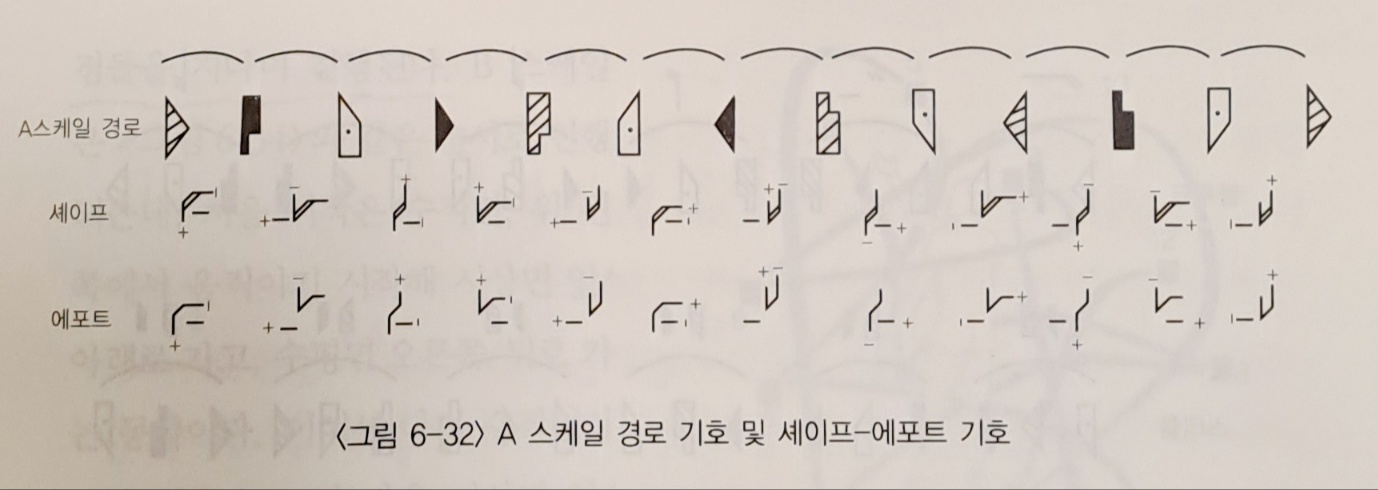
- B scale : 정육면체의 대각선 중 '튕기기/ 누르기 디아고널'의 반대축인 '미끄러지/ 내리베기 디아고널'을 피하면서 나머지 세 개의 대각선 주위를 돌면서 만들어 진다. A 스케일과 완벽한 대칭을 이루는 꼭지점들을 지나며 진행된다.
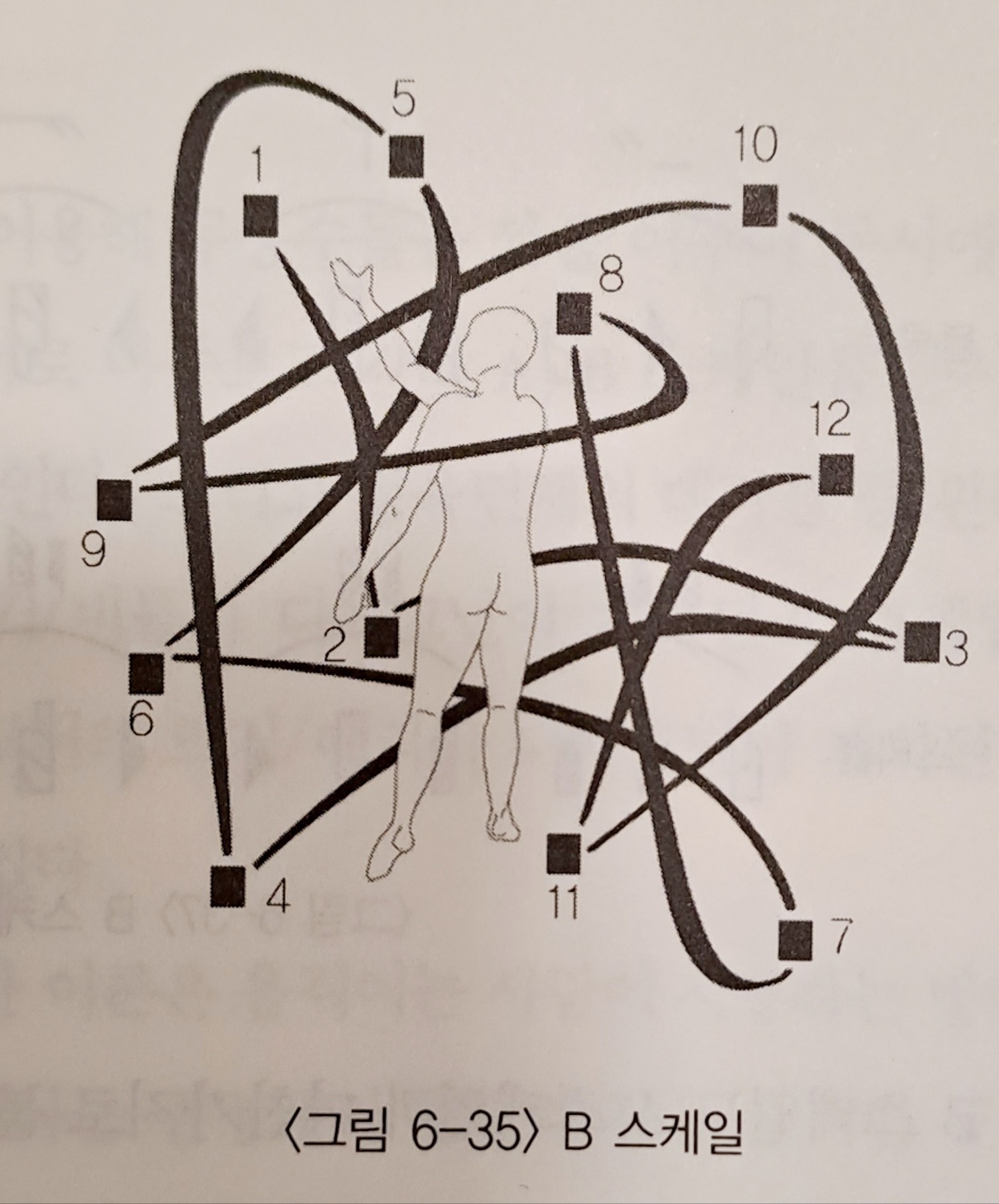
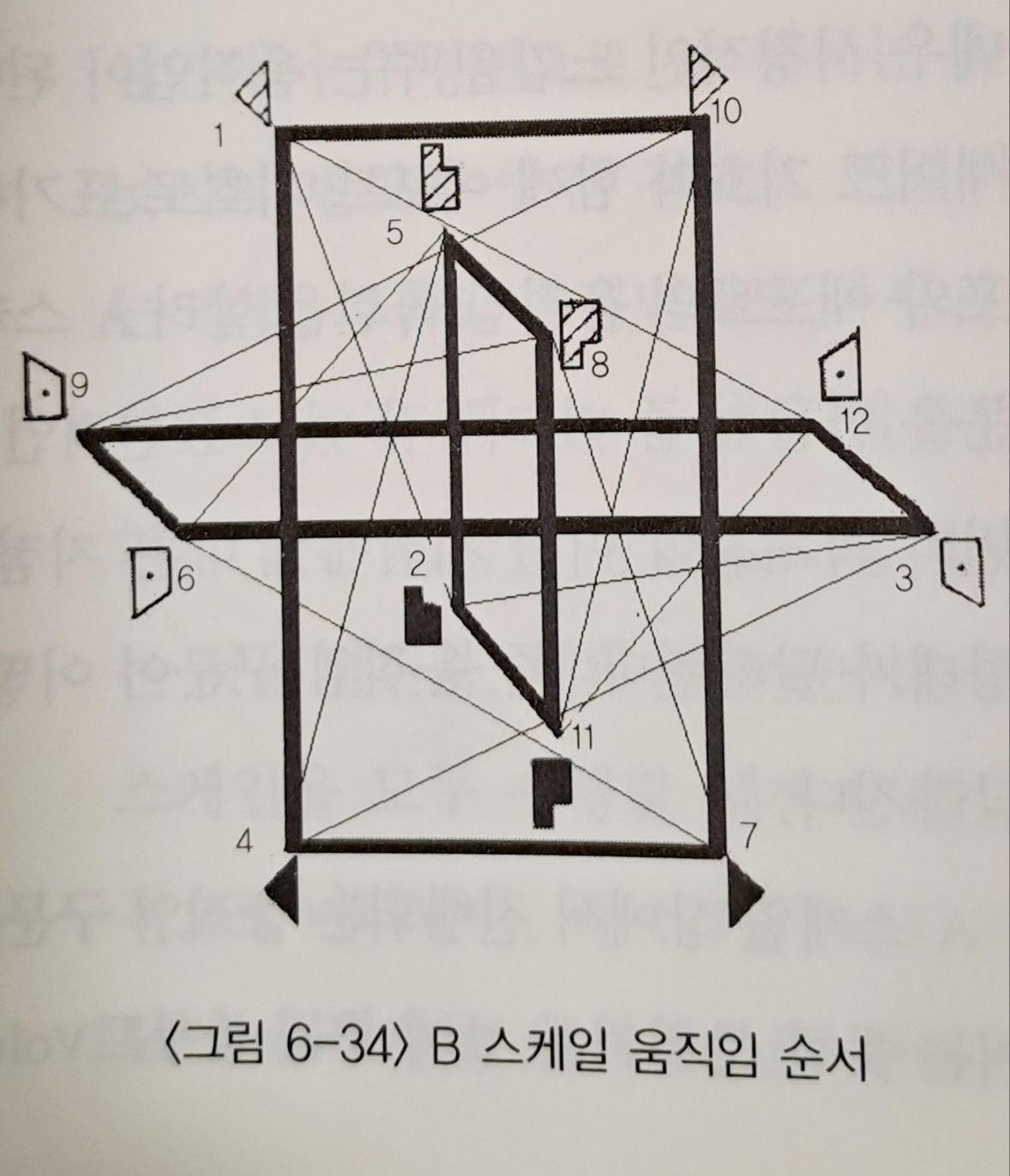
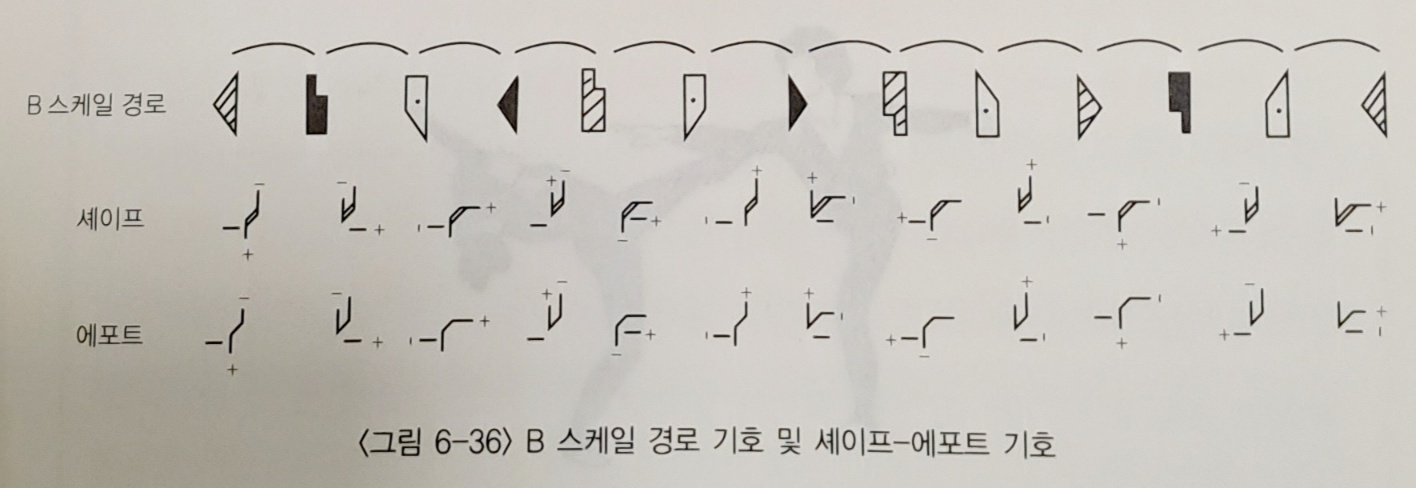
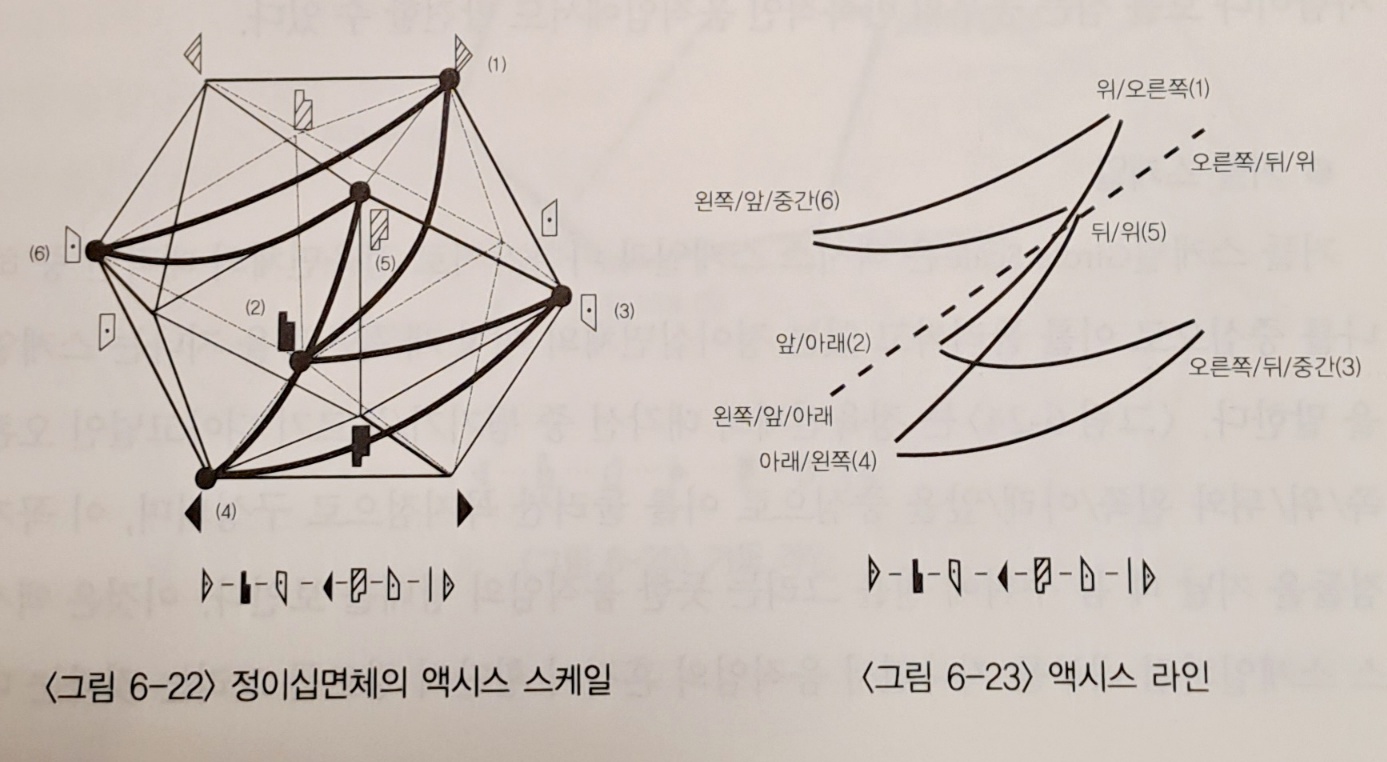
- Axis scale : 정육면체의 네 개 대각선을 중심으로 각각의 Axis 스케일을 만들 수 있다. 수직면, 수평면, 시상면에 있는 꼭지점을 차례로 지나면서 움직인다.. 움직임의 선으로 그려지는 이것은 중심적 경로와 주변적 경로 사이를 통과하는 6개의 횡단적 경로(transverse pathway)로 이루어진다..
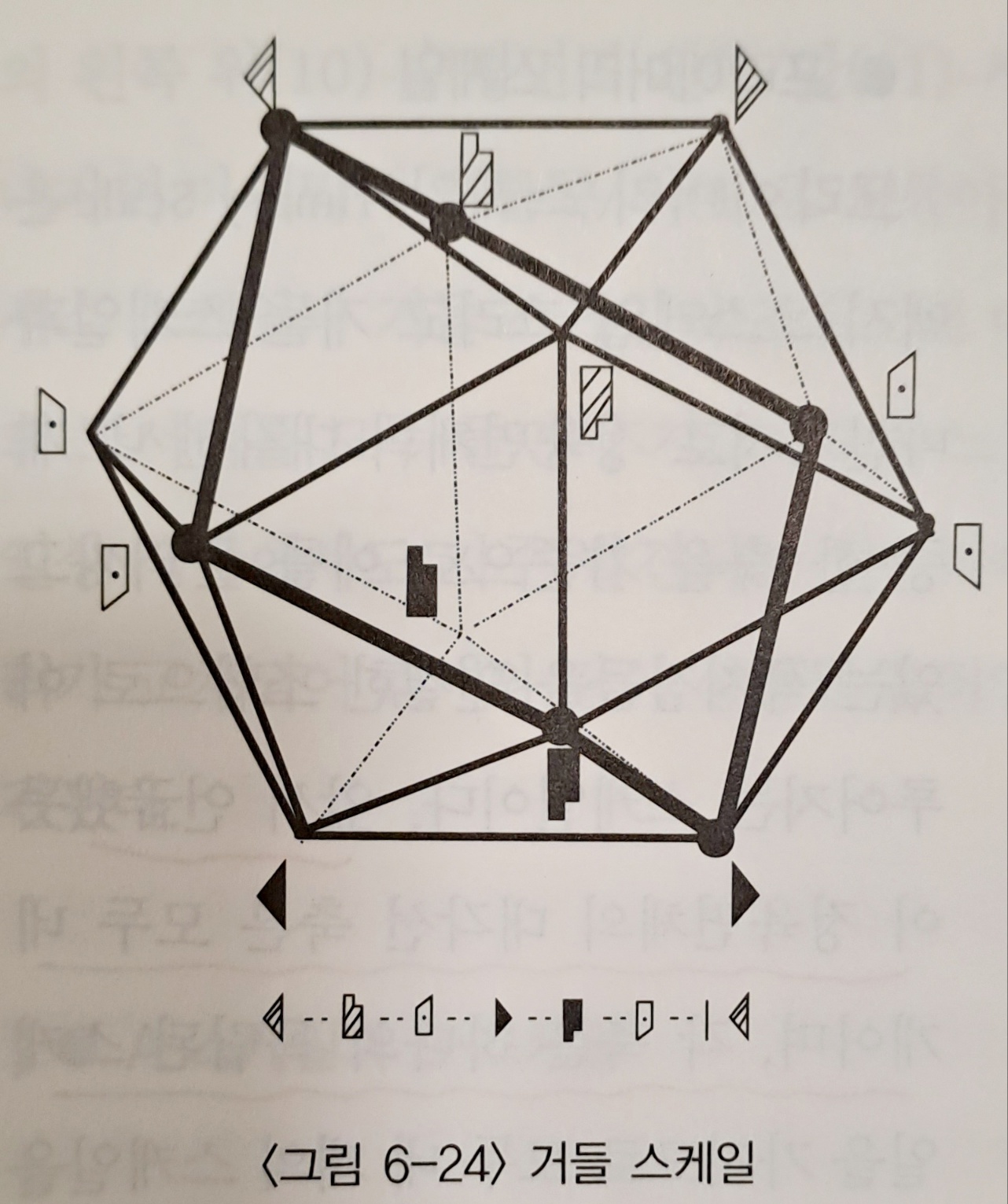
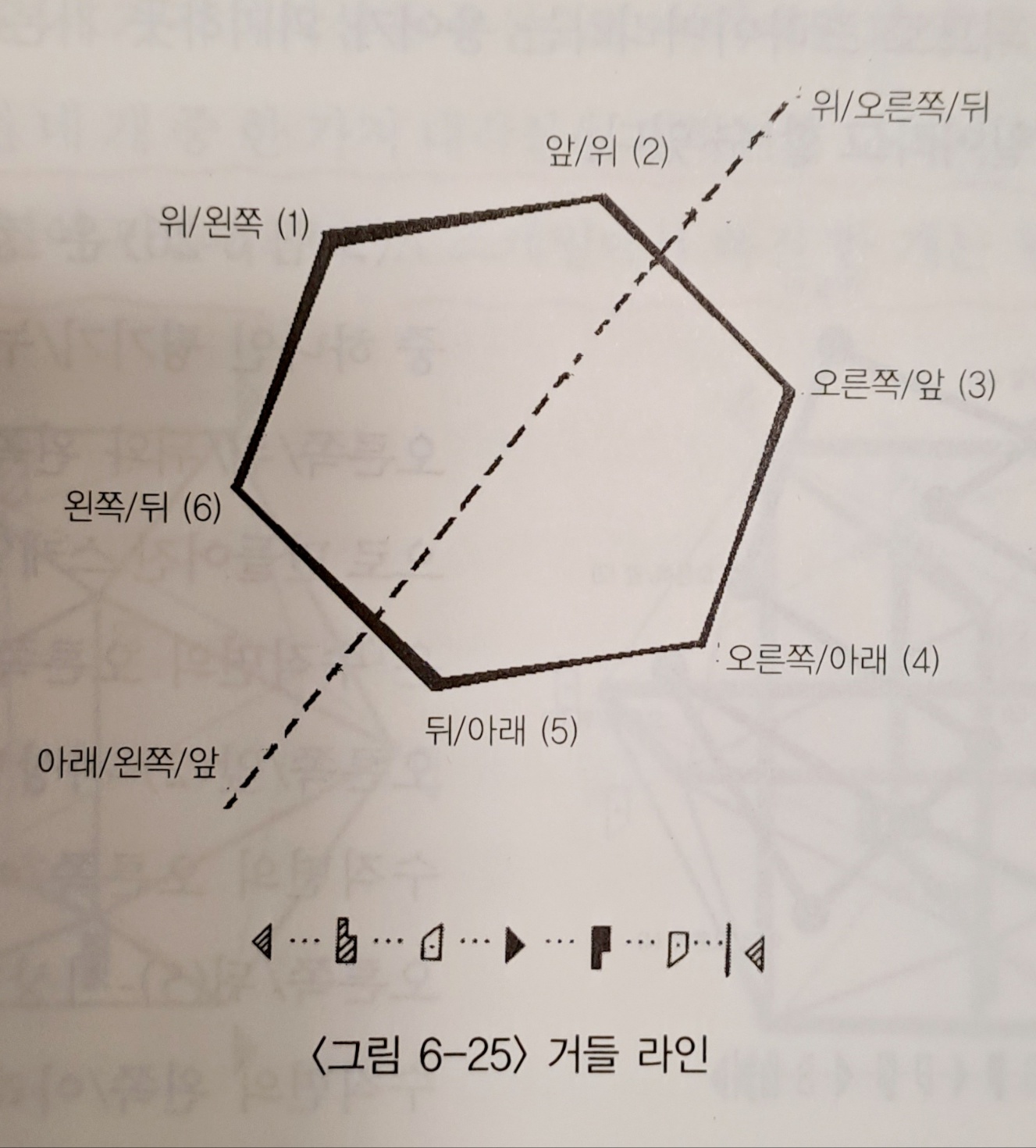
- Girdle scale : 정육면체의 대각선 중 하나를 중심으로 이를 둘러싸고 있는 정이십면체의 6개의 꼭지점을 지나는 스케일을 말한다. 내부를 지나면서 움직임의 흔적이 횡단적 경로를 그리는 것과는 다르게 정이십면체의 외부에서 주변적 경로를 그리며 일어나는 움직임이다.
신상미, 김재리 (2010). 몸과 움직임 읽기. 이화여자대학교출판부.
'리서치 > 자료 A' 카테고리의 다른 글
| Laban Sources 09 (0) | 2023.04.07 |
|---|---|
| Laban Sources 08 (0) | 2023.04.02 |
| 몸과 움직임 읽기 02 (Body, Effort) (0) | 2023.03.27 |
| 몸과 움직임 읽기 01 (0) | 2023.03.27 |
| Labanotation (0) | 2023.03.25 |